Inkognito - Sequential Bayesian Identity Disclosure
Abstract
We provide Bayesian decision support for revealing the identity of
opponents in the board game Inkognito. This includes the use of
combinatorics to deduce the likelihood of observing a particular
configuration and a sequential Bayesian belief updating scheme to infer
opponent’s identity. From a R point of view we use base R where it’s
best: manipulating matrices and supplement this with modern
dplyr style manipulation of data frames and
magrittr pipes for sequential belief updating.
/pic696789.jpg)
Image from boardgamegeek.com by yzemaze available under a CC BY-NC-SA 3.0 license.
 This work is licensed under a Creative Commons
Attribution-ShareAlike 4.0 International License. The
markdown+Rknitr source code of this blog is available under a GNU General Public
License (GPL v3) license from github.
This work is licensed under a Creative Commons
Attribution-ShareAlike 4.0 International License. The
markdown+Rknitr source code of this blog is available under a GNU General Public
License (GPL v3) license from github.
Introduction
Inkognito is a board game for four players first published in 1988. Each player has a secret identity (either Lord Fiddlebottom, Madame Zsa Zsa, Col. Bubble or Agent X) and moves four figures around the game board (a tall, a short, a fat, and a thin figure). However, only one of the figures (the player’s so called build type) is the player, the other three are smokescreen, i.e. friendly spies serving to confuse the other players. As part of the game one has to learn the identity and build of the other players in order to solve a mission goal. To this end the players move on the board, whenever one of the four figures meets one of the figures of an opponent, the opponent has to reveal information about their identity and build. There is a further neutral character, the so called ambassador, which can be moved by all players. There are two types of revelations depending on which figures meet:
- Player question: The player can decide to ask the opponent about either identity or build. If the question is about the identity the player has to state two (of the four) identities and one (of the four) builds. At least one of the three statements has to be correct, for example, if the opponent is Agent X and has the thin figure, then the statement could be: I’m Lord Fiddlebottom or Madame Zsa Zsa and have the thin figure. Conversely, if the question is build then two builds and one identity is stated – again at least one of the statements has to be true.
- Ambassador question about either identity or build: If about identity the opponent has to state two identities, one of them has to be correct. Similarly if the question is about build.
The information arising from each question is logged on a so called worksheet as shown below. The picture shows the logged information a game where the player asked one opponent (the red figure) a total of three questions (two player questions and one ambassador question).
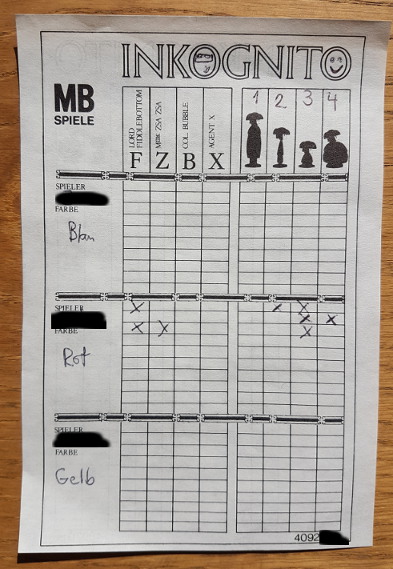
The idea is to sequentially guide your questioning in order to reveal the identity of the other players and their build. For a more detailed description of the game see this review or this even longer review. In what follows, we shall be less interested in all the particularities of the game and focus on the sequential belief update of identity and build from the questions, which is central part of the game.
Statistical Approach to the Belief Updating
We cast the questioning into mathematical notation as follows. Let \(I\in \{1,2,3,4\}\) be the opponent’s identity and \(B=\{1,2,3,4\}\) the opponent’s build. Let
\[ D_k=(I_{k,1},I_{k,2},I_{k,3},I_{k,4},B_{k,1},B_{k,2},B_{k,3},B_{k,4})' \]
be the information the opponent offers the \(k\)’th time the person is asked about the identity. Here, \(I_{k,j}\) is an indicator variable showing whether in the \(k\)’th question the opponent claims to have identity \(j\). Furthermore, \(B_{k,j}\) is an indicator variable showing whether the opponent in the \(k\)’th question claims to have aspect \(j\). Altogether \(D_k\) corresponds to one row of information in the worksheet. In what follows we address the two types of questions, the resulting likelihoods and how a Bayesian framework can be used to update the belief about the opponent’s identity and build.
Player question about identity or aspect
A player question consists of asking the opponent about either their identity or build. In response the opponent has to provide 3 pieces of information: if asked about the identity two of the statements have to concern the identity and one the build. Similarly, if asked about the build, one identity and two build statements have to be given. In other words, if the question is about identity, the vector \(D_k\) has to be such that \(\sum_{j=1}^4 I_{k,j} = 2\) and \(\sum_{c=1}^4 B_{k,c} = 1\). Furthermore, at least one of the three statements provided needs to be true, i.e. if the opponent has identity \(i\) and build \(b\), then the provided information has to be such that
\[ \begin{align*} \sum_{j=1}^4 I(I=i) I_{k,j} + \sum_{c=1}^4 I(B=b) B_{k,c} \geq 1 &\Leftrightarrow I_{k,i} + B_{k,b} \geq 1. \end{align*} \]
Ambassador question
If instead a player moves the ambassador on the same location as another player’s figure, then one can – as before – inquire about the other player’s identity or build. However, when the ambassador asks one has to provide two statements about the inquired aspect – of which one has to be true. In other words, the answer to an ambassador question \(D_k\) will be such that the sum over either the identity indicators or the builds equal 2. Furthermore, again assuming that the opponent’s true identity is \(i\) and true build is \(b\) we must have
\[ I_{k,i} + B_{k,b} = 1, \]
because the answer will either be to identity or build.
Implementation in R
We implement the possible configurations \(D_k\) on the worksheet as a matrix. Base R code does this very effectively:
##Factor levels of identities and builds
identities <- paste0("I",1:4)
builds <- paste0("B",1:4)
##Make a matrix containing all levels
M <- expand.grid(identity=1:4,build=1:4,
I1=0:1,I2=0:1,I3=0:1,I4=0:1,B1=0:1,B2=0:1,B3=0:1,B4=0:1) %>%
as.matrix
head(M,2)## identity build I1 I2 I3 I4 B1 B2 B3 B4
## [1,] 1 1 0 0 0 0 0 0 0 0
## [2,] 2 1 0 0 0 0 0 0 0 0##Subset only to valid configurations
iRows <- 3:6
bRows <- 7:10
##Player questions about identity or build
pqI <- (rowSums(M[,iRows]) == 2) & (rowSums(M[,bRows]) == 1)
pqB <- (rowSums(M[,iRows]) == 1) & (rowSums(M[,bRows]) == 2)
##Ambassafor questions about identity or build
aqI <- (rowSums(M[,iRows]) == 2) & (rowSums(M[,bRows]) == 0)
aqB <- (rowSums(M[,iRows]) == 0) & (rowSums(M[,bRows]) == 2)
##At least one of the provided information has to be correct,
##i.e. I_{k,i_true} or A_{k,b_true} has to be one.
atleast1 <- (M[cbind(1:nrow(M),M[,1]+2)] + M[cbind(1:nrow(M),M[,2]+6)]) >= 1
##Restrict matrix to all valid answers
Mprime <- data.frame(M, atleast1=atleast1, pqI=pqI, pqB=pqB, aqI=aqI, aqB=aqB) %>%
filter(pqI | pqB | aqI | aqB)
##Additional column containing the identity build combination
Mprime %<>% mutate(ib=paste0("I",identity,"/B",build)) %>%
select(ib, everything())
##Show 3 random rows to get an impression
Mprime[sample(1:nrow(Mprime), size=3), ]## ib identity build I1 I2 I3 I4 B1 B2 B3 B4 atleast1 pqI pqB aqI aqB
## 783 I3/B4 3 4 0 0 1 0 1 0 0 1 TRUE FALSE TRUE FALSE FALSE
## 769 I1/B1 1 1 0 0 1 0 1 0 0 1 TRUE FALSE TRUE FALSE FALSE
## 308 I4/B1 4 1 1 0 0 0 1 1 0 0 TRUE FALSE TRUE FALSE FALSELikelihood
Considering the possible answers to a player question and assuming that the true opponent values are \((i,b)\), then the opponent for a player question can choose between one of a total of 15 valid combinations:
- Assuming the identity will be correct in the revealed information,the opponent has to choose one of three remaining identities for the second information about identity and needs to pick between one of four builds to report (3*4=12 possible combinations).
- Assuming the build of the revealed information is correct, but
not the identity, then the opponent has to choose 2 of the 3
remaining identities for the identity part of the revealed information
(
choose(3,2)=3 combinations).
Hence, the total number of possible valid combinations is 15, that is the likelihood for each valid combination is 1/15. For a given provided combination \(D_k\) and \((i,b)\) we thus need to check if \(D_k\) is valid given \((i,b)\). If not the likelihood is zero, if valid, then the likelihood is 1/15.
For an ambassador question about identity, the opponent has to choose their true identity and one of the three other identities, i.e. the likelihood is easily found to be \(1/3\), if the opponent is indifferent about which of the three identities to report back. Altogether, given our own identity \((i,b)\) we thus need to check if \(D_k\) is possible given \((i,b)\). If this is not the case then likelihood is zero, otherwise the likelihood is 1/15.
Likelihood Implementation in R
This is conveniently done using either an apply to the
rows or – allowing for a more readable way using the column names –
using a dplyr mutate statement:
##Compute likelihood for each valid answer (assuming indifference between choices)
Mprime %<>% mutate(prob = if_else(!atleast1, 0,
if_else(aqI | aqB, 1/3, 1/15)))Prior
The prior distribution consists of the joint prior \(P(I=i, B=b)\) for all 4*4=16 combinations of identity and build. For easier vector multiplication we flatten the table into a vector. In the particular game, from which the above worksheet originates, the player with the worksheet was \(I=4\) and \(B=2\), hence, we assign these states the probability zero.
##Factor levels of identities and builds
identities <- paste0("I",1:4)
builds <- paste0("B",1:4)
##Generate levels of joint table of identity and build
ib_combs <- as.character(outer(identities, builds, paste, sep="/"))
##Generate joint table based on player's identity
prior <- structure(as.numeric(outer(c(1/3,1/3,1/3,0), c(1/3,0,1/3,1/3))),names=ib_combs)
prior## I1/B1 I2/B1 I3/B1 I4/B1 I1/B2 I2/B2 I3/B2 I4/B2 I1/B3
## 0.1111111 0.1111111 0.1111111 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.1111111
## I2/B3 I3/B3 I4/B3 I1/B4 I2/B4 I3/B4 I4/B4
## 0.1111111 0.1111111 0.0000000 0.1111111 0.1111111 0.1111111 0.0000000Furthermore, we create a small helper function
p_marginal allowing us to compute the marginal
distributions of identity and build, respectively, from the joint
distribution. That is \(P(I=i)=\sum_{b=1}^4
P(i,b)\) and \(P(B=b)=\sum_{i=1}^4
P(i,b)\).
This allows us to compute:
p_marginal(prior, what="I")## I1 I2 I3 I4
## 0.3333333 0.3333333 0.3333333 0.0000000p_marginal(prior, what="B")## B1 B2 B3 B4
## 0.3333333 0.0000000 0.3333333 0.3333333Posterior
For \(i=1,\ldots, 4\) and \(b=1,...,4\) we can compute the posterior distribution using Bayes’ theorem: \[ \begin{align*} P(I=i,B=b\>|\>D_k) &= \frac{P(D_k|\>I=i,B=b)P(I=i,B=b)}{P(D_k)} \\ &= \frac{P(D_k|\> I=i,B=b)P(I=i,B=b)}{\sum_{j=1}^4 \sum_{c=1}^4 P(D_k|\> I=j,B=c)P(I=j,B=c)}. \end{align*} \] In code:
#############################################################
## Function for sequentially updating the state information
############################################################
update <- function(prior, Dk) {
##Sanity check
stopifnot(names(prior) == ib_combs)
##Configurations matching the observed data Dk
idx <- apply(Mprime[, grep("I+|B+", names(Mprime))], 1, function(x) all(x==Dk))
##Extract likelihood and put it in same order as the ib_combs vector
##for prior and likelihood vectors to match in order of the entries
vector_idx <- pmatch(ib_combs, Mprime[idx,]$ib)
lik <- (Mprime[idx,]$"prob")[vector_idx]
##Compute P(I=i,B=b|D_k), i.e. our updated belief
belief <- lik * prior / sum(lik * prior)
return(belief)
}We use the data from the above shown worksheet, combine it with our prior and thus update our belief of which identity and build the opponent has.
##The three data lines of the worksheet
D <- bind_rows(data.frame(I1=1,I2=0,I3=0,I4=0,B1=0,B2=1,B3=1,B4=0),
data.frame(I1=0,I2=0,I3=0,I4=0,B1=0,B2=0,B3=1,B4=1),
data.frame(I1=1,I2=1,I3=0,I4=0,B1=0,B2=0,B3=1,B4=0))
##Sequential belief updating (we use a version using pipes)
prior %>% update(D[1,]) %>% update(D[2,]) %>% update(D[3,]) -> beliefThe above way of piping is a nice way to illustrate the sequential aspect of the inference!
##Show results
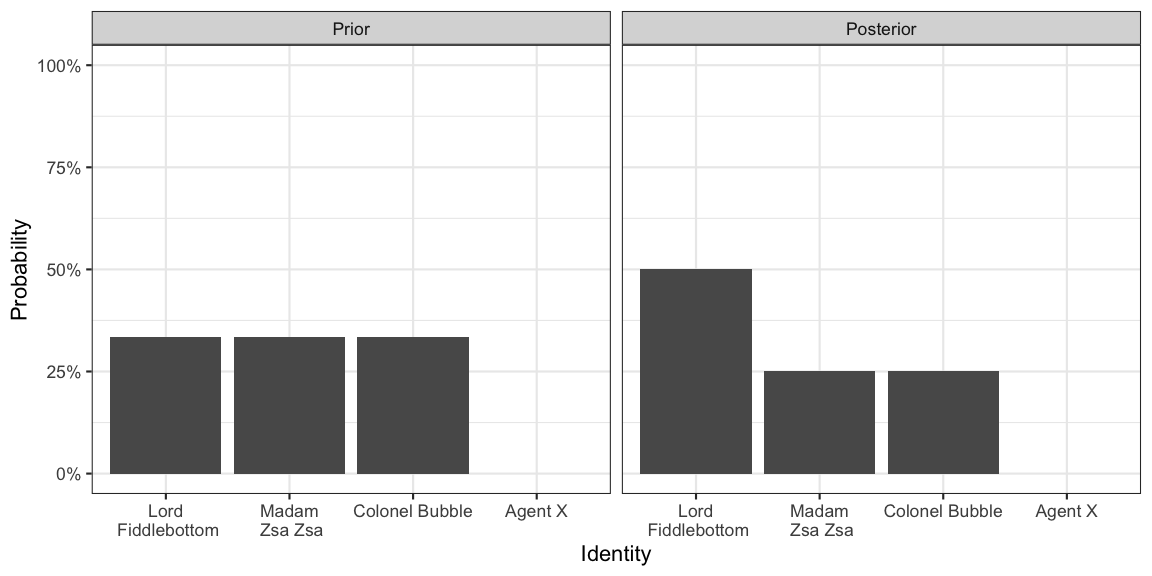
p_marginal(belief, what="I")## I1 I2 I3 I4
## 0.50 0.25 0.25 0.00p_marginal(belief, what="B")## B1 B2 B3 B4
## 0.00 0.00 0.75 0.25Based on these results we are somewhat certain that the player has identity 1, i.e. is Lord Fiddlebottom, and has build 3, i.e. is the fat figure. The belief update can also be visualized as shown below for identity.
Discussion
After the end of the particular game the above worksheet is from, it turned out that the opponent was \(I=1\) and \(B=4\). Altogether, the opponent was not too impressed by the decision support provided by this post: That identity 1 was most likely appears natural when simply counting the number of crosses for this identity on the worksheet. Same goes for the build, however, she was deliberately attempting to fool the player by providing the impression that she was build 3. As always with statistics, heuristics can take you part of the way, however, simply counting crosses would for example not reveal that identity 3 still also is an option. Furthermore, the slyness of misinformation is not handled by the combinatorical approach towards calculating the likelihood, because it is assumed that every valid choice is equally likely. To this end, more games need to be played in order to learn the opponent’s confusion strategy and adapt the probabilities to reflect these strategies. Finally, in longer games, one would have answers from several opponents and this would be combined in one model, because knowing opponent 1 is Lord Fiddlebotom certainly also helps to rule out some options for opponent 2.
So what is next: If time permits, a shiny app allowing the user to fill in their worksheet and calculate and visualize the subsequent belief about each opponent’s identity and build.