Abstract

Unexploded WWII bombs are ticking threats despite being dropped more than 70 years ago. In this post we explain how statistical methods are used to plan the search and disposal of unexploded WWII bombs. In particular we consider and exemplify the non-parametric nearest neighbour distance (NND) method implemented in the R package highriskzone. The method analyses the spatial pattern of exploded bombs to determine so called risk-zones, that is regions with a high likelihood of containing unexploded bombs. The coverage of such risk-zones is investigated through both non-parametric and parametric point process simulation.

NCAP aerial photo from 1944 showing the bombing of the V2 rocket facility at Peenemünde, Germany. Image is available under a custom NCAP license - higher resolution images are available from NCAP.


Creative Commons License This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License. The markdown+Rknitr source code of this blog is available under a GNU General Public License (GPL v3) license from github.

\[ \newcommand{\bm}[1]{\boldsymbol{\mathbf{#1}}} \]

Introduction

During WWII Germany was pounded with about 1.5 mio tons of bombs of which about 10-15% did not explode. More than 70 years after the end of WWII these unexploded bombs (UXBs) still pose a threat and are the frequent cause of large scale evacuations to secure their safe disposal when found. Luckily, lethal incidents are rare thanks to a huge effort to localise and safely dismantle UXBs. As part of this effort, aerial photos taken by the allies after the attacks provide valuable information about the possible locations of UXBs. Some UXBs are directly visible in the photos - see for example the green circles in this NCAP image or p. 6 in the following information flyer by one of the companies offering such aerial identification services (featured in this news article). In other cases the photos only provide information about the location of the exploded bombs. This information can be used to identify areas where there is a high likelihood of UXBs. Such areas would then be carefully scrutinized using on-the-ground search methods, for example, electromagnetic and magnetic detectors.

The aim of Mahling, Höhle, and Küchenhoff (2013) was to develop statistical methods for the identification of such risk-zones in co-operation with Oberfinanzdirektion Niedersachsen, which supports the removal of unexploded ordnance in federal properties in Germany. In what follows we will discuss one of the methods used in the paper, the so called nearest neighbourhood distance method and illustrate its implementation in the R package highriskzone originally created by Heidi Seibold and now maintained by Felix Günther.

Mathematical Setup

Casting matters into mathematical notation: Let \(X\) be a point process denoting the spatial locations of all bombs dropped in the particular window of interest \(W \subseteq \mathbb{R}^2\). Furthermore, let \(Y\) denote the observed point process of exploded bomb and \(Z=X\backslash Y\) the point process of unexploded bombs. Note that only the process \(Y\) is observed; \(Z\) is not observed and the target of our inference. We assume that the probability \(q\) of a dropped bomb not exploding is homogeneous in \(W\). Thus if \(X\) is a inhomogeneous Poisson point process with intensity function \(\lambda_X(\bm{s})\), \(\bm{s}\in W\), then

\[ \lambda_Y(\bm{s}) = (1-q) \lambda_X(\bm{s}) \quad \text{and}\quad \lambda_Z(\bm{s}) = q \lambda_X(\bm{s}) \]

are the intensity functions of \(Y\) and \(Z\), respectively.

The figure below shows \(Y\) for an actual observed WWII bomb point consisting of n=443 bombs available from the R package highriskzone (Seibold et al. 2017). The observation window contains a particular area of interest for which a risk assessment needs to be done - often these contain a known WWII military target, e.g., an airport, an arms factory or a military casern. In order to not disclose the exact location of the considered area, coordinates are given relative to an arbitrary origo. In reality one would closely link such digitized aerial images to other terrain features using a GIS system.

library(highriskzone)
library(spatstat)
data(craterA)
summary(craterA)
## Planar point pattern:  443 points
## Average intensity 0.0001082477 points per square unit
## 
## Coordinates are given to 4 decimal places
## 
## Window: polygonal boundary
## single connected closed polygon with 208 vertices
## enclosing rectangle: [0, 2334.3758] x [0, 2456.4061] units
## Window area = 4092470 square units
## Fraction of frame area: 0.714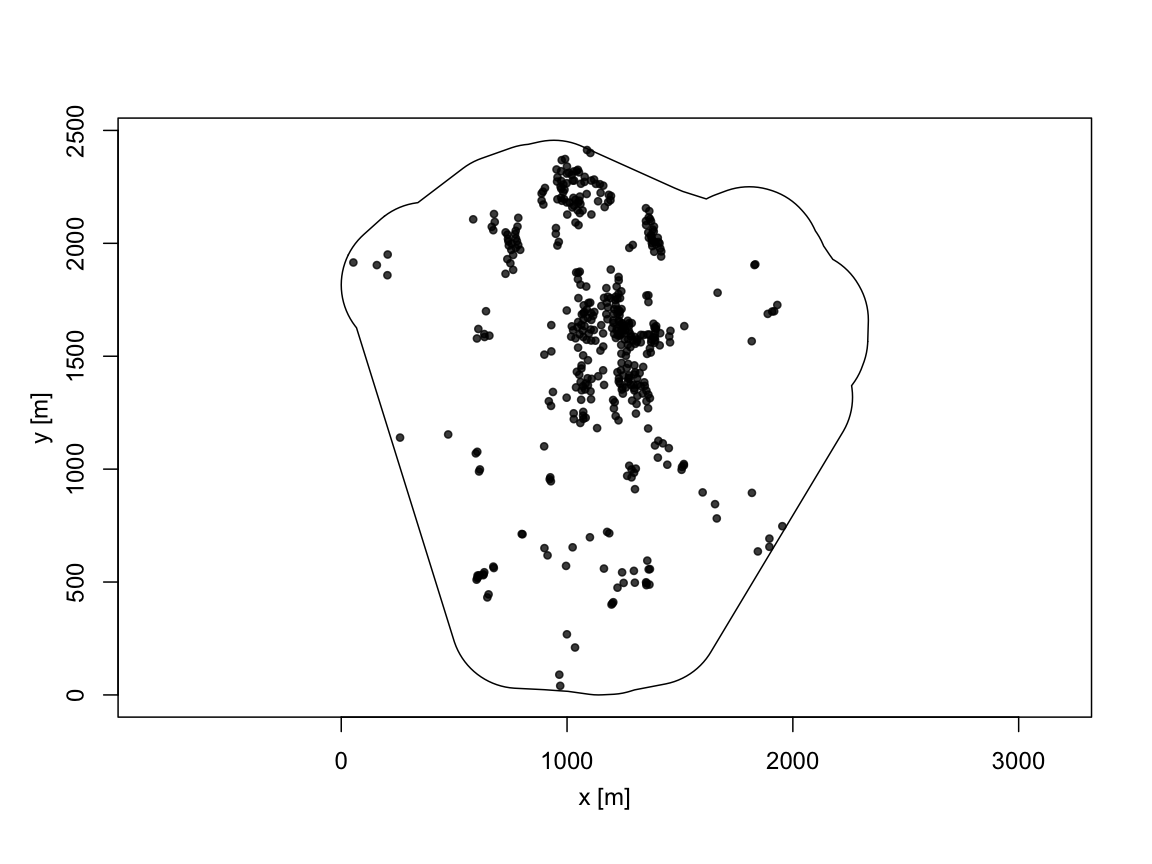

Observed bomb point pattern ($Y$) within the observation window $W$. The point pattern craterA corresponding to an instance of the process \(Y\) is provided in R as an object of class ppp from the R package spatstat (Baddeley, Rubak, and Turner 2015). Instead of inferring the locations in \(Z\) directly, we shall be interested in determining a region within \(W\), a so called high risk zone, which with a high likelihood contains the points of \(Z\). We shall consider two methods for this job: a non-parametric method based on nearest neighbour distances in \(Y\) and an intensity function based inhomogeneous Poisson process approach incorporating \(q\).

High Risk Zones

A heuristic way to determine a high-risk zone is the following: Determine the distribution function \(D\) of the nearest neighbour distance (NND) distribution based on the 443 points in the point pattern. Use the distribution to determine a desired quantile, say \(0 \leq p \leq 1\) of the NND distribution. Denoting the \(p\) sample quantile of the NND distribution by \(Q(p)\), a \(p\)-quantile NND based high-risk zone is then obtained as the union of putting a disc of radius \(x_q\) around each observed exploded bomb in \(Y\) - in mathematical terms:

\[ R_p = \left(\bigcup_{\bm{y} \in Y} B(\bm{y}, Q(p))\right) \bigcap W = \left\{\bm{s} \in W : \min_{\bm{y}\in Y} || \bm{s} − \bm{y} || \leq Q_Y(p) \right\}, \]

where \(B(\bm{s}, r)\) denotes a disc of radius \(r\) around the point \(\bm{s}\) and \(||\bm{s} - \bm{y}||\) is the distance between the two points \(\bm{s}\) and \(\bm{y}\). The intersection with \(W\) is done in order to guarantee that the risk zone lies entirely within \(W\). As an example, we would determine the 99%-quantile NND zone for craterA using spatstat functionality as follows:

(Qp <- quantile(nndist(craterA), p = 0.99, type = 8))
##      99% 
## 142.1391
dmap <- distmap(craterA)
zone_dist <- eval.im( dmap < Qp )

The above can also be done directly using highriskzone::det_hrz function:

zone_dist <- det_hrz(craterA, type="dist", criterion = "indirect", cutoff=0.99)

Either way, the resulting risk-zone is as follows:

summary(zone_dist)
## high-risk zone of type dist  
## criterion: indirect  
## cutoff: 0.99  
##  
## threshold: 142.1391  
## area of the high-risk zone: 2580654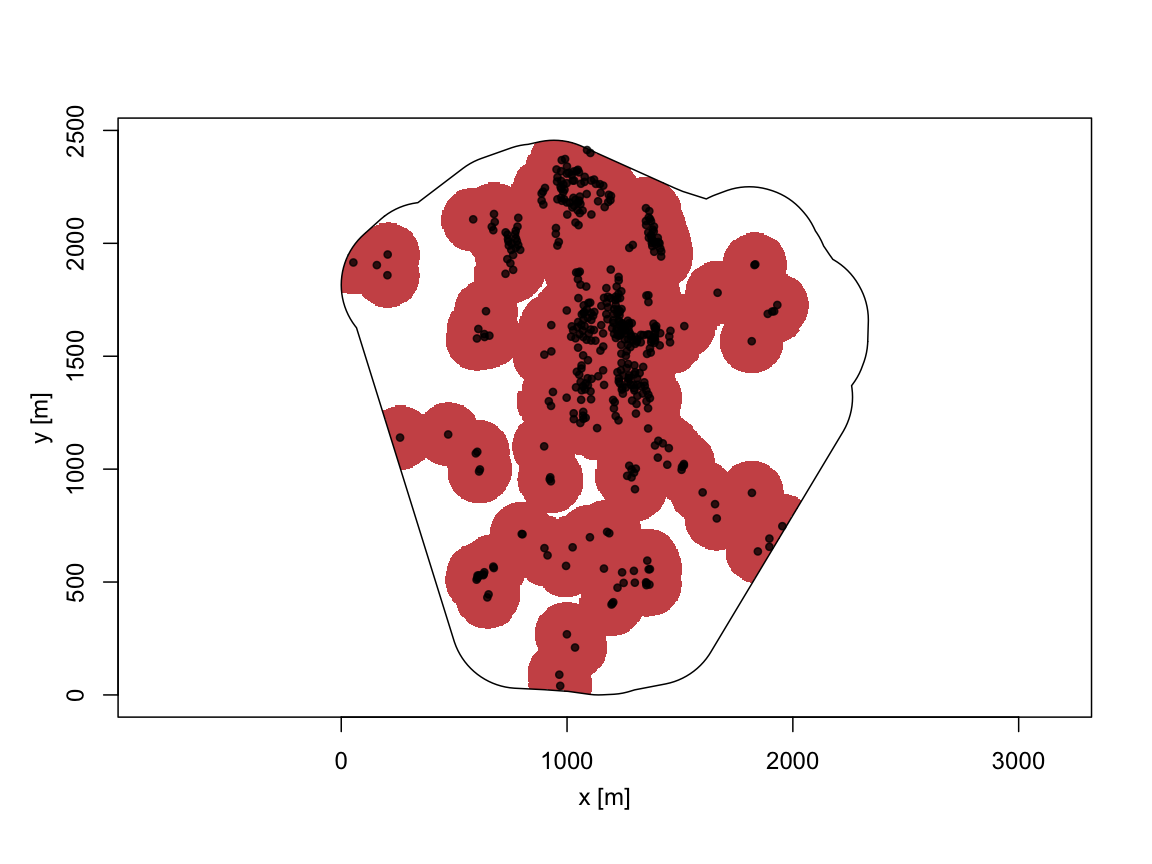

Mahling, Höhle, and Küchenhoff (2013) show that risk zones constructed by the NND method work surprisingly well despite lacking a clear theoretical justification. One theoretical issue is, for example, that the NND distribution function determined by the above method is for the \((1-q)\) thinned process \(Y\), even though the actual interest is in the process \(X=Y\cup Z\). Because of the thinning one would typically have that \(D_Y(r) \leq D_X(r)\) and thus \(Q_Y(p) > Q_X(p)\). Using \(Q_Y(p)\) to make statements about \(X\) (and thus \(Z\)) is therefore slightly wrong. However, this error cancels, because we then use the points in \(Y\) to add a buffer of radius \(Q_Y(p)\). Had we instead used the smaller, but true, \(Q_X(p)\) the risk zone would have gotten a too small, because \(X\) would also have contained more points to form discs around than \(Y\). The method thus implicitly takes \(q\) non-parametrically into account, because its NND is determined based on \(Y\) and subsequently discs of radius \(Q_Y(p)\) are formed around the points of \(Y\).

Technical details you might want to skip: The above feature is most easily illustrated if \(X\) is a homogeneous Poisson process with intensity \(\lambda_X\). In this case we have that the NND distribution function is (p.68, Illian et al. 2008)

\[ D_X(r) = 1 - \exp(-\lambda_X \pi r^2), \quad r>0. \]

Also note that \(D_Y(r) = 1 - \exp(-(1-q)\lambda_X \pi r^2)\) and therefore \(D_Y(r) > D_X(r)\). Now solving for the \(p\)-quantile of the NND in this homogeneous Poisson case means solving

\[ Q_Y(p) = \min_{r\geq 0} \{ D_Y(r) \geq p \} \Leftrightarrow Q_Y(p) = \sqrt{ \frac{\log(1-p)}{\lambda_Y \pi}}. \]

From this it becomes clear than in the homogeneous Poisson case \(Q_ Y(p)\) is a factor \(\sqrt{1/(1-q)}\) larger than \(Q_X(p)\), which is the actual target of interest.

Assessing the coverage of a risk-zone

Two criterion appear immediate in order to assess the coverage of a risk-zone \(R\):

  1. The probability \(p_{\text{out}}\) that there will be at least one bomb outside the risk zone, i.e. \(P( N( Z \backslash R) > 0)\), where \(N(A)\) denotes the number of events in the set \(A \subseteq W\). Note: this probability is depending heavily on the amount of points in \(Z\), the more points there are, the higher is \(p_{\text{out}}\). However, it reflects the idea “one miss is all it takes to get in trouble”.

  2. The proportion of events in \(Z\) not located in \(R\), i.e. \(N( Z \backslash R) / N(Z)\), we shall denote this criterion by \(p_{\text{miss}}\). Note: This probability is taking possible different sizes of \(Z\) into account, but also takes a more relative approach towards how many bombs are not covered by the zone.

Under the assumption of independence between whether \(Z\)-events are within or outside the risk-zone one can convert back and forth between \(p_{\text{miss}}\) and \(p_{\text{out}}\) by

\[ p_{\text{out}} = P( N( Z \backslash R) > 0) = 1- P(N(Z \backslash R) = 0) \approx 1 - (1-p_{\text{miss}})^{N(Z)}, \]

where one in a simulation setup would know \(Z\) and thus also \(N(Z)\). Note that for a \(p\)-quantile NND risk-zone we expect \(1-p_{\text{miss}}\) to be approximately equal to \(p\). We can investigate the behaviour of risk-zones according to the two above criterion through the use of simulation. Either by simply \(q\)-thinning of the existing point pattern \(Y\) and then use this thinned pattern to determine a risk-zone, which is then evaluated. An alternative approach is to estimate the intensity surface from \(Y\), upscale it to get the intensity of \(X\), simulate \(X\) as an inhomogeneous Poisson point process with this intensity surface, thin this pattern to get a simulated instance of \(Y\), construct the risk-zone based on this pattern and then evaluate the coverage of the zone (Mahling, Höhle, and Küchenhoff 2013). Note that this type of simulation is based on more assumptions compared to the non-parametric thinning simulation approach.

We generate 1,000 realizations of \(Y\) and \(Z\) through \(q\)-thinning of the original craterA pattern while computing the coverage measures for the NND method as follows:

suppressPackageStartupMessages(library(doParallel))
registerDoParallel(cores=4)

simulate_method <- "thinning" #"intensity" # "cond_intensity"
sim <- foreach(i=seq_len(getDoParWorkers()), .combine=rbind) %dopar% {
  tryCatch(
    eval_method(craterA, type=c("dist"), criterion=c("indirect"),
                cutoff=0.99, numit = 250, simulate=simulate_method,
                pbar=FALSE),
    error= function(e) return(NULL))
}
## # A tibble: 1 x 5
##   p_out  p_miss `1-p_miss` p_out_derived    nZ
##   <dbl>   <dbl>      <dbl>         <dbl> <dbl>
## 1 0.097 0.00236      0.998        0.0996  44.4

The numbers state the average p_out and p_missin the 1000 simulations. Furthermore, nZ denotes the average number of events in \(Z\). We see that the NND method performs even a little better than intended, because \(1-p_{\text{miss}}\) is even higher than the intended \(p\)=99%. The probability that the risk-zone misses at least one bomb lies as low as 0.097. This is quite close to the above described approximate conversion from \(p_{\text{miss}}\) (0.100 vs. 0.097). Changing the simulation method for \(X\) to that of an inhomogeneous Poisson process with intensity \(1/(1-q) \cdot \hat{\lambda}_Y(\bm{s})\) yields similar results:

## # A tibble: 1 x 5
##   p_out  p_miss `1-p_miss` p_out_derived    nZ
##   <dbl>   <dbl>      <dbl>         <dbl> <dbl>
## 1 0.352 0.00897      0.991         0.361  49.6

We note that the probability of missing at least one bomb is much higher under this parametric simulation method. Only a small fraction of this is explained by \(Z\) now consisting of more points. A likely explanation is that the parametric model is only semi-adequate to describe how the point patterns form. Therefore, the new \(X\) might have a somewhat different neighbourhood distribution than anticipated.

To compare more specifically with the intensity function based risk-zone method of Mahling, Höhle, and Küchenhoff (2013) we use a specification, where the risk-zone derived by the NND method or the intensity method have the same area (250 hectare).

sim_area <- foreach(i=seq_len(getDoParWorkers()), .combine=rbind) %dopar% {
  tryCatch(
    eval_method(craterA, type=c("dist","intens"), criterion=rep("area",2),
                cutoff=rep(2500000,2), numit = 100,
                simulate=simulate_method, pbar=FALSE),
    error= function(e) return(NULL))
}
## # A tibble: 2 x 6
##   Type   p_out  p_miss `1-p_miss` p_out_derived area_zone
##   <fct>  <dbl>   <dbl>      <dbl>         <dbl>     <dbl>
## 1 dist   0.123 0.00278      0.997         0.117  2500009.
## 2 intens 0.55  0.0172       0.983         0.539  2499994.

For the particular example we see an advantage of using the NND method, because both p_out p_miss are much lower for the intensity based method. Again, this might be due to the intensity method being based on assumptions, which for the particular example do not appear to be so adequate. Results in Mahling (2013) were, however, much better for this example (c.f. Tab 2), which could be an indication that there is a problem in the highriskzone package implementation of this method?

Discussion

Being a statistician is fascinating, because the job is the entry ticket to so many diverse research fields. The proposed methods and evaluations helped the Oberfinanzdirektion obtain a quantitative framework to decide which methods to use in their routine risk-assessment. Further details on the above application can be found in Mahling, Höhle, and Küchenhoff (2013) as well as in Monia’s Ph.D. dissertation (Mahling 2013). Note also that the techniques are not limited to UXB detection: Infer-unknown-points-from-a-thinned-process problems occur both in 1D and 2D point processes in a range of other fields, e.g., under-reporting of infectious disease locations or in the calculation of animal abundance in ecology.

As a personal anecdote: When finishing the work on Mahling, Höhle, and Küchenhoff (2013) I was in transition from university to working at a public health institute. The deal was to finish the UXB work partly in spare-time and partly in the new work time. To honour this I added my new work place as second affiliation before submitting, but as part of the institution’s internal clearing procedure of the publication, I was asked to remove this affiliation again by the higher management, because the work ‘had nothing to do with public health’. While its questionable whether exploding bombs really do not have a public health impact, a few months later, I ended up using very similar statistical techniques to model occurred-but-not-yet-reported cases during a critical infectious disease outbreak (Höhle and an der Heiden 2014).

Grand Slam bomb exploding near Arnsberg viaduct 1945

Literature

Baddeley, A., E. Rubak, and R. Turner. 2015. Spatial Point Patterns: Methodology and Applications with R. London: Chapman; Hall/CRC. http://www.crcpress.com/books/details/9781482210200/.
Höhle, M., and M. an der Heiden. 2014. “Bayesian Nowcasting During the STEC O104:H4 Outbreak in Germany, 2011.” Biometrics 70 (4): 993–1002. https://doi.org/10.1111/biom.12194.
Illian, J., A. Penttinen, H. Stoyan, and D. Stoyan. 2008. Stistical Analysis and Modelling of Spatial Point Patterns. Wiley.
Mahling, M. 2013. “Determining High-Risk Zones by Using Spatial Point Process Methodology.” PhD thesis, Department of Statistics, University of Munich. https://edoc.ub.uni-muenchen.de/15886/1/Mahling_Monia.pdf.
Mahling, M., M. Höhle, and H. Küchenhoff. 2013. “Determining high-risk zones for unexploded World War II bombs by using point process methodology.” Journal of the Royal Statistical Society, Series C 62 (2): 181–99. https://doi.org/10.1111/j.1467-9876.2012.01055.x.
Seibold, H., M. Mahling, S. Linne, and F. Günther. 2017. Highriskzone: Determining and Evaluating High-Risk Zones. https://cran.r-project.org/web/packages/highriskzone/index.html.